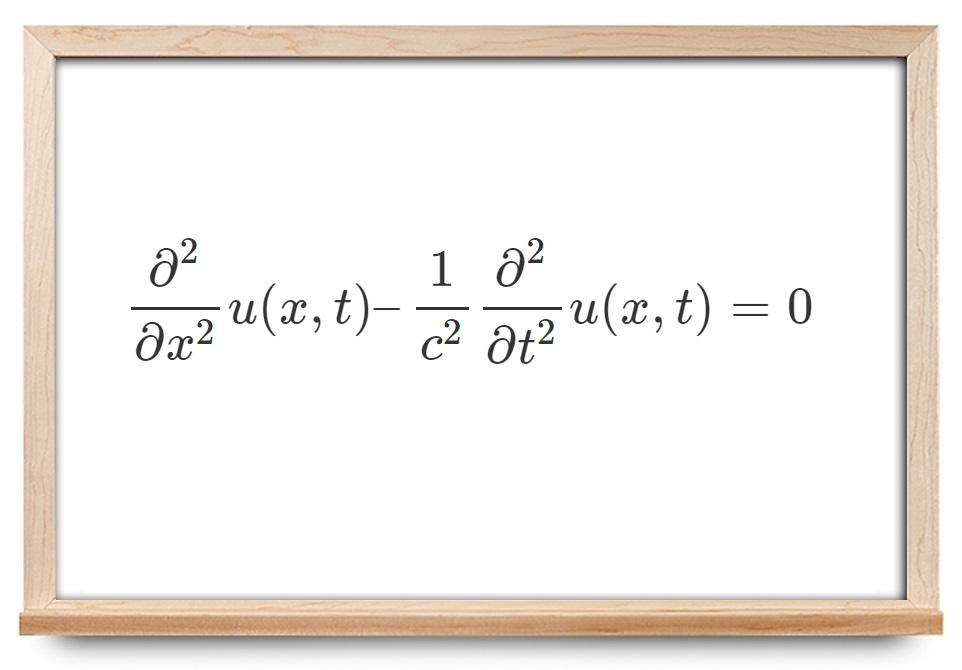روش دالامبر، یکی از برجستهترین و کارآمدترین روشهای عددی در تحلیل ریاضی و علوم محاسباتی محسوب میشود. این روش به مدد سادگی و کاراییاش، توانسته است در بسیاری از زمینههای علمی و مهندسی جایگاه ویژهای بیابد. دالامبر، ریاضیدان و فلسفهدان فرانسوی قرن هجدهم، با توسعه این روش، به ما امکان میدهد تا معادلات پیچیده را با دقت بیشتری مورد بررسی قرار دهیم. در این مقاله، به بررسی ویژگیها، مزایا و کاربردهای روش دالامبر خواهیم پرداخت و نشان خواهیم داد که چگونه این روش میتواند ابزاری کلیدی در حل مسائل مختلف علمی و عملی باشد. با ما همراه باشید تا به دنیای ریاضیات و علم دالامبر سفر کنیم و با جنبههای ناگفته این روش آشنا شویم.
روش دالامبر و اصول بنیادی آن در علم آمار
روش دالامبر به عنوان یکی از تکنیکهای بنیادی در علم آمار، به تحلیل و تفسیر دادهها کمک میکند. این روش به ویژه در بررسی سریهای زمانی و پیشبینی روندهای آینده کاربرد دارد. از ویژگیهای اصلی این تکنیک میتوان به موارد زیر اشاره کرد:
- تحلیل ساختار دادهها: دالامبر به ما امکان میدهد تا بستر اصلی دادهها را شناسایی کنیم.
- مدلسازی پیشبینی: با استفاده از روش دالامبر، میتوانیم پیشبینیهای دقیقی از تحولات آینده داشته باشیم.
- تجزیه و تحلیل همبستگی: این روش میتواند روابط بین متغیرهای مختلف را کشف کند.
اصول بنیادی این تکنیک مبتنی بر مفهوم احتمال و توزیعهای آماری است. در واقع، دالامبر معتقد بود که با استفاده از دادههای موجود میتوان به بهترین شکل ممکن نتایج را پیشبینی کرد. از این رو، یک جدول ساده میتواند ابعاد مختلفی از روش دالامبر را به تصویر بکشد:
| عنصر | توضیح |
|---|---|
| توزیع احتمال | تحلیل احتمال وقوع رویدادها. |
| مدلهای آماری | استفاده از مدلهای مختلف برای شبیهسازی دادهها. |
| پیشبینی | استفاده از دادههای گذشته برای پیشبینی آینده. |

کاربردهای عملی روش دالامبر در تحلیل دادهها
روش دالامبر به عنوان یک ابزار تحلیلی، کاربردهای بسیار متنوعی در زمینههای مختلف دادهکاوی و تحلیل دادهها دارد. این روش عمدتاً برای ارائه و تجزیه و تحلیل توزیعهای احتمالی استفاده میشود و میتواند در حوزههای زیر مؤثر واقع گردد:
- تحلیل خطرات مالی: با استفاده از روش دالامبر، میتوان برای ارزیابی و تحلیل ریسکهای احتمالی در بازارهای مالی و سرمایهگذاریها استفاده کرد.
- مدلسازی پیشبینی: این روش به درک بهتر روندها و الگوها در دادههای زمانی، به ویژه در پیشبینی رویدادهای آینده کمک میکند.
- بهینهسازی فرآیندها: در بهینهسازی فرآیندهای صنعتی و تجاری، دالامبر به شناسایی نقاط قوت و ضعف در دادهها کمک میکند.
علاوه بر این، روش دالامبر میتواند در تحقیقات علمی و اجتماعی نیز به عنوان ابزاری مؤثر برای تحلیل دادههای پیچیده به کار گرفته شود. به عنوان مثال، در بررسی تغییرات اجتماعی یا اقتصادی، این روش قادر است الگوهای معنادار و تفاوتهای قابل توجهی را در دادهها نشان دهد:
| جنبههای کاربردی | مزایا |
|---|---|
| اقتصاد | تحلیل روندهای اقتصادی و پیشبینی بحرانها |
| بهداشت و درمان | تحلیل نتایج درمانی و شناسایی الگوهای علائم بیماری |
| بازار کار | تحلیل تغییرات شغلی و نیازهای بازار کار |

مدلسازی دادهها با بهرهگیری از روش دالامبر
مدلسازی دادهها با روش دالامبر به عنوان یکی از تکنیکهای نوین در علم دادهها شناخته میشود که تحت اصل دالامبر، به استفاده از ویژگیهای ریاضی و منطقی برای تحلیل و پردازش دادهها میپردازد. در این روش، دادهها به طور سیستماتیک و با استفاده از الگوریتمهای خاص، به شکل قابل تحلیل تبدیل میشوند. از این رو، میتوان به موارد زیر اشاره کرد:
- دقت بالای تحلیل: با بهرهگیری از روش دالامبر، میتوان به دقت بالاتری در نتیجهگیریهای خود دست یافت.
- مدلهای پیچیده: این روش امکان ساخت مدلهای پیچیدهتری را فراهم میکند که میتواند به تحلیل عمیقتر دادهها منجر شود.
- کاهش خطا: تجزیه و تحلیل صحیح و منطقی دادهها باعث کاهش خطا در نتایج نهایی میشود.
یکی از مزایای مهم این روش، قابلیت سازگاری آن با انواع دادهها و شرایط مختلف است. از دادههای طبقهبندیشده گرفته تا دادههای پیوسته، روش دالامبر میتواند به بهترین شکل ممکن به پردازش آنها بپردازد. همچنین، این روش در کاربردهای عملی مانند تجزیه و تحلیل بازار، پیشبینی روندها و شبیهسازی سیستمها کاربرد دارد. برای درک بهتر نقاط قوت و ضعف این روش، میتوان جدولی به شرح زیر را بررسی کرد:
| مزایا | معایب |
|---|---|
| دقت و صحت بالا | پیچیدگی بالای مدلها |
| قابلیت انطباق با دادههای مختلف | نیاز به متخصصین با تجربه |
| توانایی تحلیل دادههای بزرگ | هزینههای بالای پیادهسازی |
نکات کلیدی برای بهبود دقت نتایج با استفاده از دالامبر
برای بهبود دقت نتایج با استفاده از روش دالامبر، رعایت چند نکته کلیدی بسیار اهمیت دارد. اولین نکته، جمعآوری دادههای دقیق و معتبر است. اطمینان حاصل کنید که اطلاعات مورد استفاده شما از منابع معتبر و بهروز انتخاب شده است. همچنین، تحلیلگر باید تسلط کافی بر روش و تکنیکهای آماری مربوط به دالامبر داشته باشد تا بتواند به بهترین نحو از این روش بهرهبرداری کند. آموزش و جلسات کاری میتوانند به تقویت تواناییهای تحلیلگر کمک کنند.
نکته دوم، تنظیم صحیح پارامترهای ورودی است. برای مثال، انتخاب اندازه مناسب دادهها و ارزیابی متغیرهای مختلف میتواند تأثیر زیادی بر دقت نتایج داشته باشد. همچنین، استفاده از ابزارهای تحلیلی و نرمافزارهای مناسب برای اجرای این روش بسیار ضروری است. در نهایت، توجه به واحدهای اندازهگیری و استانداردسازی آنها، موجب میشود تا دادههای شما با دقت بالایی تحلیل شوند.
سوال و جواب
سوالات و پاسخها درباره “روش دالامبر”
سوال ۱: روش دالامبر چیست و چه کاربردی دارد؟
پاسخ: روش دالامبر یکی از تکنیکهای اصلی در ریاضیات و به ویژه در تحلیل عددی است که برای حل معادلات دیفرانسیل و همچنین در مسائل مربوط به انتگرالگیری عددی به کار میرود. این روش برگرفته از یک روند تکراری است که به به دست آوردن تخمینی نزدیک به جواب دقیق کمک میکند.
سوال ۲: اساسنامه و اصول پایهای این روش چگونه است؟
پاسخ: روش دالامبر بر پایه استفاده از دو مقدار ابتدایی است که به تدریج به یک جواب دقیق نزدیک میشوند. در این رویکرد، با استفاده از مقادیر مثبت و منفی و عملیات ضرب و جمع، فضایی میسازیم که در آن میتوانیم به روند تخمین نزدیک شویم. این روند گاهی ممکن است چندین بار تکرار شود تا به نتایج مطلوب برسیم.
سوال ۳: چه مزایایی در استفاده از روش دالامبر وجود دارد؟
پاسخ: یکی از مزایای اصلی روش دالامبر، سادگی و قابلیت فهم آسان آن است. همچنین، این روش میتواند در بسیاری از مسائل ریاضی و علمی به کار گرفته شود و به راحتی به الگوریتمهای کامپیوتری انتقال یابد. سرعت انجام محاسبات و دقت بالای نتایج در شرایط مناسب، از دیگر نکات مثبت این روش به شمار میآید.
سوال ۴: آیا محدودیتهایی نیز در استفاده از این روش وجود دارد؟
پاسخ: بله، یکی از محدودیتهای بزرگ روش دالامبر این است که در برخی حالات خاص، به خصوص در مسائل پیچیده یا غیرخطی، ممکن است به سرعت به جواب دست نیابد یا حتی نتیجه نادرستی به دست آورد. همچنین، انتخاب مناسب مقادیر ابتدایی میتواند تأثیر زیادی بر روی موفقیت این روش داشته باشد.
سوال ۵: روش دالامبر در کجاها موفقت بیشتری داشته است؟
پاسخ: روش دالامبر به طور ویژه در علوم مهندسی، فیزیک و اقتصاد کاربرد گستردهای دارد. برای مثال، در تحلیل سازهها و بررسی رفتار دینامیکی سیستمها، این روش میتواند نتایج دقیقی ارائه دهد. در علوم کامپیوتری نیز، برای حل مسائل بهینهسازی و یادگیری ماشین، از این روش بهرهبرداری میشود.
سوال ۶: آیا منابع خاصی برای یادگیری بیشتر درباره این روش وجود دارد؟
پاسخ: بله، چندین کتاب و مقاله علمی وجود دارند که به تفصیل به روش دالامبر و کاربردهای آن پرداختهاند. همچنین، دورههای آنلاین و ویدیوهای آموزشی نیز در این زمینه تهیه شدهاند که میتوانند کمک فراوانی به علاقهمندان نمایند. از این رو، پیشنهاد میشود به منابع معتبر علمی و آموزشی مراجعه شود.
سوال ۷: آیا میتوان روش دالامبر را با دیگر روشها مقایسه کرد؟
پاسخ: بله، روش دالامبر میتواند با دیگر روشهای عددی مانند روش نیوتن-رافسون یا روش بیزی مقایسه شود. هر یک از این روشها مزایا و معایب خود را دارند و انتخاب بهترین روش بستگی به نوع مسئله و نیازهای خاص آن دارد. به عنوان مثال، روش نیوتن برای مسائل خاصی که به مقدار دقیقتری نیاز دارند، مناسبتر است، در حالی که روش دالامبر میتواند برای تخمینهای اولیه مؤثرتر باشد.
—
این سوالات و پاسخها میتوانند به شما کمک کنند تا درک بهتری از روش دالامبر و کاربردهای آن پیدا کنید.
In Conclusion
در پایان، روش دالامبر بهعنوان یکی از تکنیکهای بارز و نوآورانه در حل معادلات دیفرانسیل نشاندهنده قدرت علم ریاضیات در تبیین و تحلیل مسائل پیچیده است. این روش نه تنها به ما ابزاری برای یافتن راهحلهای دقیق و کارآمد میدهد، بلکه درک بهتری از ساختار و رفتار سیستمهای مختلف را به ما ارائه میکند. با پیوند دادن اصول مختلف ریاضی و کاربردهای آنها در زمینههای علمی و مهندسی، میتوانیم همچنان از این روش برای حل چالشهای جدید و پیشرفت در علم و فناوری بهرهبرداری کنیم. امید است که این مقاله، شما را با ابعاد مختلف روش دالامبر آشنا کرده و الهامبخش شما در سفرهای علمیتان باشد.